Electrons in a 3-dimensional box (cuboid)¶
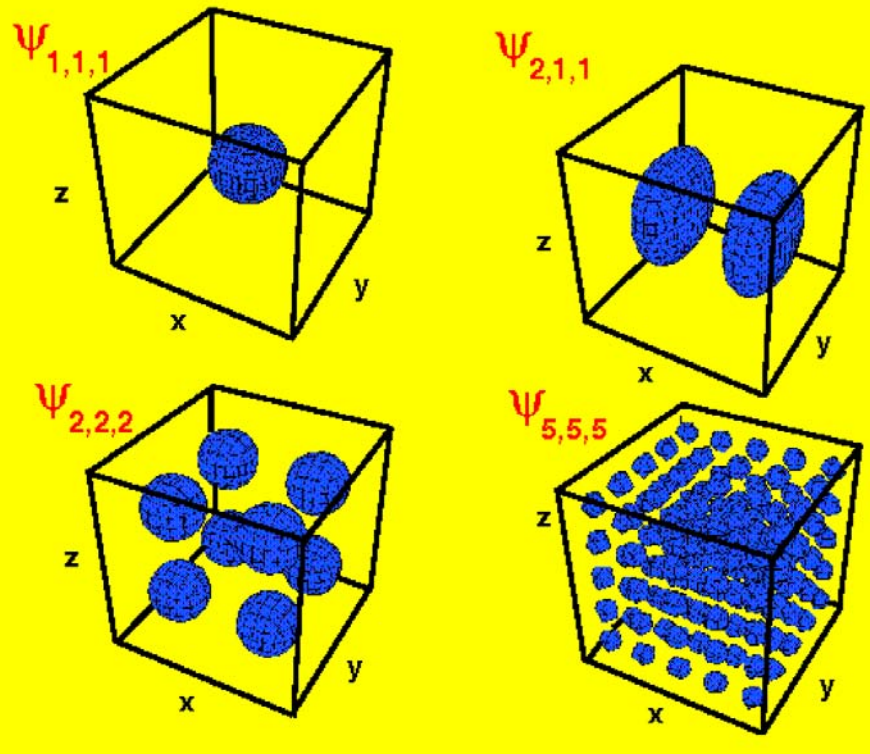
Suppose that particles are confined to a cuboid (or rectangular prism) with side-lengths $a_x$, $a_y$, and $a_z$. Then the Schrödinger equation is:
$$
\left[-\frac{\hbar^2}{2m}\left( \frac{d^2}{dx^2} + \frac{d^2}{dy^2} + \frac{d^2}{dz^2} \right) + V(x,y,z) \right]\psi_{n_x,n_y,n_z}(x,y,z) = E_{n_x,n_y,n_z} \psi_{n_x,n_y,n_z}(x,y,z)
$$
where
$$
V(x,y,z) =
\begin{cases}
+\infty & x\leq 0 \text{ or }y\leq 0 \text{ or }z\leq 0 \\
0 & 0\lt x \lt a_x \text{ and } 0 \lt y \lt a_y \text{ and } 0 \lt z \lt a_z \\
+\infty & a_x \leq x \text{ or } a_y \leq y \text{ or } a_z \leq z
\end{cases}
$$
There are three quantum numbers because the system is three-dimensional.
The three-dimensional second derivative is called the Laplacian, and is denoted
$$
\nabla^2 = \frac{d^2}{dx^2} + \frac{d^2}{dy^2} + \frac{d^2}{dz^2} = \nabla \cdot \nabla
$$
where
$$
\nabla = \left[ \frac{d}{dx}, \frac{d}{dy}, \frac{d}{dz} \right]^T
$$
is the operator that defines the gradient vector. The 3-dimensional momentum operator is
$$
\hat{\mathbf{p}} = i \hbar \nabla
$$
which explains why the kinetic energy is given by
$$
\hat{T} = \frac{\hat{\mathbf{p}} \cdot \hat{\mathbf{p}}}{2m} = \frac{\hbar^2}{2m} \nabla^2
$$
As with the 2-dimensional particle-in-a-rectangle, the 3-dimensional particle-in-a-cuboid can be solved by separation of variables. Rewriting the Schrödinger equation as:
$$
\left[\left(-\frac{\hbar^2}{2m} \frac{d^2}{dx^2} + V_x(x) \right)
+\left(-\frac{\hbar^2}{2m} \frac{d^2}{dy^2} + V_y(y) \right)
+\left(-\frac{\hbar^2}{2m} \frac{d^2}{dz^2} + V_z(z) \right) \right]\psi_{n_x,n_y,n_z}(x,y,z) = E_{n_x,n_y,n_z} \psi_{n_x,n_y,n_z}(x,y,z)
$$
where
$$
V_x(x) =
\begin{cases}
+\infty & x\leq 0\\
0 & 0\lt x \lt a_x\\
+\infty & a_x \leq x
\end{cases} \\
V_y(y) =
\begin{cases}
+\infty & y\leq 0\\
0 & 0\lt y \lt a_y\\
+\infty & a_y \leq y
\end{cases} \\
V_z(z) =
\begin{cases}
+\infty & z\leq 0\\
0 & 0\lt z \lt a_z\\
+\infty & a_z \leq z
\end{cases}
$$
By the same logic as we used for the 1-dimensional particle in a box, we can deduce that the ground-state wavefunction for an electron in a cuboid is:
$$
\psi_{n_x n_y n_z}(x,y,z) = \frac{2\sqrt{2}}{\sqrt{a_x a_y z_z}} \
\sin\left(\tfrac{n_x \pi x}{a_x}\right) \sin\left(\tfrac{n_y \pi y}{a_y}\right)\sin\left(\tfrac{n_z \pi z}{a_z}\right) \qquad \qquad n_x=1,2,3,\ldots;n_y=1,2,3,\ldots;n_z=1,2,3,\ldots
$$
The corresponding energy is thus:
$$
E_{n_x n_y n_z} = \frac{h^2}{8m}\left(\frac{n_x^2}{a_x^2}+\frac{n_y^2}{a_y^2}+\frac{n_z^2}{a_z^2}\right)\qquad \qquad n_x,n_y,n_z=1,2,3,\ldots
$$
As before, especially when there is symmetry, there are many degenerate states. For example, for a particle-in-a-cube, where $a_x = a_y = a_z = a$, the first excited state is three-fold degenerate since:
$$
E_{2,1,1} = E_{1,2,1} = E_{1,1,2} = \frac{6h^2}{8ma^2}
$$
There are other states of even higher degeneracy. For example, there is a twelve-fold degenerate state:
$$
E_{5,8,15} = E_{5,15,8} = E_{8,5,15} = E_{8,15,5} = E_{15,5,8} = E_{15,8,5} = E_{3,4,17} = E_{3,17,4} = E_{4,3,17} = E_{4,17,3} = E_{17,3,4} = E_{17,4,3} = \frac{314 h^2}{8ma^2}
$$

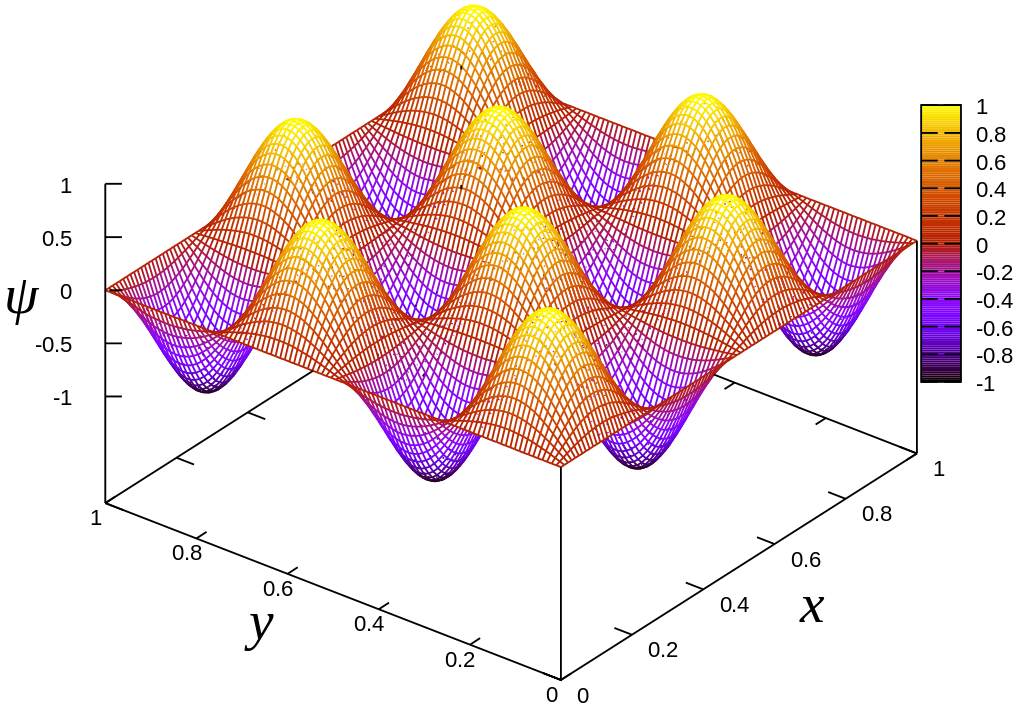 We have treated the particle in a one-dimensional box, where the (time-independent) Schrödinger equation was:
$$
\left(-\frac{\hbar^2}{2m} \frac{d^2}{dx^2} + V(x) \right)\psi_n(x) = E_n \psi_n(x)
$$
where
$$
V(x) =
\begin{cases}
+\infty & x\leq 0\\
0 & 0\lt x \lt a\\
+\infty & a \leq x
\end{cases}
$$
We have treated the particle in a one-dimensional box, where the (time-independent) Schrödinger equation was:
$$
\left(-\frac{\hbar^2}{2m} \frac{d^2}{dx^2} + V(x) \right)\psi_n(x) = E_n \psi_n(x)
$$
where
$$
V(x) =
\begin{cases}
+\infty & x\leq 0\\
0 & 0\lt x \lt a\\
+\infty & a \leq x
\end{cases}
$$
 The energies of a particle confined to a circular disk of radius $a$ are:
$$
E_{n,l} = \frac{\hbar^2 x_{n,l}^2}{2ma^2} = \frac{h^2 x_{n,l}^2}{8 m \pi^2 a^2} \qquad \qquad n=1,2,\ldots; \quad l=0,\pm 1,\pm 2, \ldots
$$
and its eigenfunctions are:
$$
\psi_{n,l}(r,\theta) \propto J_{l}\left(\frac{x_{n,l}r}{a} \right) e^{i l \theta}
$$
where $x_{n,l}$ are the zeros of the Bessel function, $J_l(x_{n,l}) = 0$. The first zero is $x_{1,0} = 2.4048$. These solutions are exactly the resonant energies and modes that are associated with the vibration of a circular drum whose membrane has uniform thickness/density.
The energies of a particle confined to a circular disk of radius $a$ are:
$$
E_{n,l} = \frac{\hbar^2 x_{n,l}^2}{2ma^2} = \frac{h^2 x_{n,l}^2}{8 m \pi^2 a^2} \qquad \qquad n=1,2,\ldots; \quad l=0,\pm 1,\pm 2, \ldots
$$
and its eigenfunctions are:
$$
\psi_{n,l}(r,\theta) \propto J_{l}\left(\frac{x_{n,l}r}{a} \right) e^{i l \theta}
$$
where $x_{n,l}$ are the zeros of the Bessel function, $J_l(x_{n,l}) = 0$. The first zero is $x_{1,0} = 2.4048$. These solutions are exactly the resonant energies and modes that are associated with the vibration of a circular drum whose membrane has uniform thickness/density.

 The energies of a particle confined to a spherical ball of radius $a$ are:
$$
E_{n,l} = \frac{\hbar^2 y_{n,l}^2}{2ma^2} \qquad n=1,2,\ldots; \quad l=0,1,\ldots; \quad m=0, \pm1, \ldots, \pm l
$$
and its eigenfunctions are:
$$
\psi_{n,l,m}(r,\theta,\phi) \propto j_l\left(\frac{y_{n,l}r}{a} \right) Y_l^{m_l}(\theta, \phi)
$$
where $y_{n,l}$ are the zeros of the spherical Bessel function, $j_l(y_{n,l}) = 0$. The first spherical Bessel function, which corresponds to s-like solutions ($l=0$), is
$$
j_l(y) = \frac{\sin y}{y}
$$
and so
$$
y_{n,0} = n \pi
$$
This gives explicit and useful expressions for the $l=0$ wavefunctions and energies,
$$
E_{n,0} = \frac{h^2 n^2}{8 m a^2}
$$
and its eigenfunctions are:
$$
\psi_{n,0,0}(r,\theta,\phi) \propto \frac{a}{n \pi r} \sin \left( \frac{n \pi r}{a} \right)
$$
Notice that the $l=0$ energies are the same as in the one-dimensional particle-in-a-box and the eigenfunctions are very similar.
The energies of a particle confined to a spherical ball of radius $a$ are:
$$
E_{n,l} = \frac{\hbar^2 y_{n,l}^2}{2ma^2} \qquad n=1,2,\ldots; \quad l=0,1,\ldots; \quad m=0, \pm1, \ldots, \pm l
$$
and its eigenfunctions are:
$$
\psi_{n,l,m}(r,\theta,\phi) \propto j_l\left(\frac{y_{n,l}r}{a} \right) Y_l^{m_l}(\theta, \phi)
$$
where $y_{n,l}$ are the zeros of the spherical Bessel function, $j_l(y_{n,l}) = 0$. The first spherical Bessel function, which corresponds to s-like solutions ($l=0$), is
$$
j_l(y) = \frac{\sin y}{y}
$$
and so
$$
y_{n,0} = n \pi
$$
This gives explicit and useful expressions for the $l=0$ wavefunctions and energies,
$$
E_{n,0} = \frac{h^2 n^2}{8 m a^2}
$$
and its eigenfunctions are:
$$
\psi_{n,0,0}(r,\theta,\phi) \propto \frac{a}{n \pi r} \sin \left( \frac{n \pi r}{a} \right)
$$
Notice that the $l=0$ energies are the same as in the one-dimensional particle-in-a-box and the eigenfunctions are very similar.