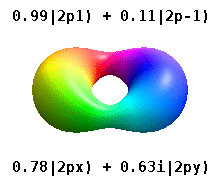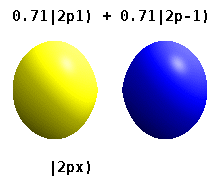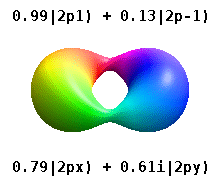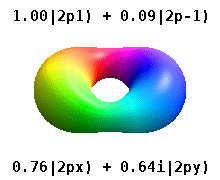Schrödinger Equation for One-Electron Atoms
Denoting the mass of the electron as $m_e$, the charge of the electron as $=e$, and the permittivity of free space as $\epsilon_0$, the Hamiltonian for the attraction of an electron to a atomic nucleus with atomic number $Z$ (and charge $+Ze$) at the origin, $(x,y,z) = (0,0,0)$, is:
$$
\hat{H}_{\text{1 el. atom}} = -\frac{\hbar^2}{2m_e} \nabla^2 - \frac{Z e^2}{4 \pi \epsilon_0 r}
$$
where $r = \sqrt{x^2+y^2+z^2}$ is the distance of the electron from the nucleus. In atomic units, the Hamiltonian is:
$$
\hat{H}_{\text{1 el. atom}} = -\tfrac{1}{2} \nabla^2 - Zr^{-1}
$$
Just as we did for the electron confined to a spherical ball, we rewrite the Schrödinger equation in spherical coordinates,
$$
\left(-\frac{1}{2} \left( \frac{d^2}{dr^2}
+ \frac{2}{r} \frac{d}{dr}\right)
+ \frac{\hat{L}^2}{2r^2} - \frac{Z}{r} \right)
\psi_{n,l,m_l}(r,\theta,\phi)
= E_{n,l,m_l}\psi_{n,l,m_l}(r,\theta,\phi)
$$
and use the fact the eigenvalues of the squared-magnitude of the angular momentum, $\hat{L}^2$ are the spherical harmonics
$$
\hat{L}^2 Y_l^{m} (\theta, \phi) = l(l+1)Y_l^{m} (\theta, \phi) \qquad l=0,1,2,\ldots m=0, \pm 1, \ldots, \pm l
$$
and the technique of separation of variables to deduce that the wavefunctions of one-electron atoms have the form
$$
\psi_{n,l,m}(r,\theta,\phi) = R_{n,l}(r) Y_l^{m}(\theta,\phi)
$$
where the radial wavefunction, $R_{n,l}(r)$ is obtained by solving the radial Schrödinger equation
$$
\left(-\frac{1}{2} \left( \frac{d^2}{dr^2}
+ \frac{2}{r} \frac{d}{dr}\right)
+ \frac{l(l+1)}{2r^2} - \frac{Z}{r} \right)
R_{n,l}(r)
= E_{n,l}R_{n,l}(r)
$$